D. Scott Rinnan, Ph.D.

D. Scott Rinnan, Ph.D.

Diversity, equity, and justice through data science.

The dispersal success and persistence of populations with asymmetric dispersal

Published in Theoretical Ecology, 2018.

Rinnan DS. "The dispersal success and persistence of populations with asymmetric dispersal." Theoretical Ecology, 11(1), 55-69. https://doi.org/10.1007/s12080-017-0348-x
Download here

Abstract:

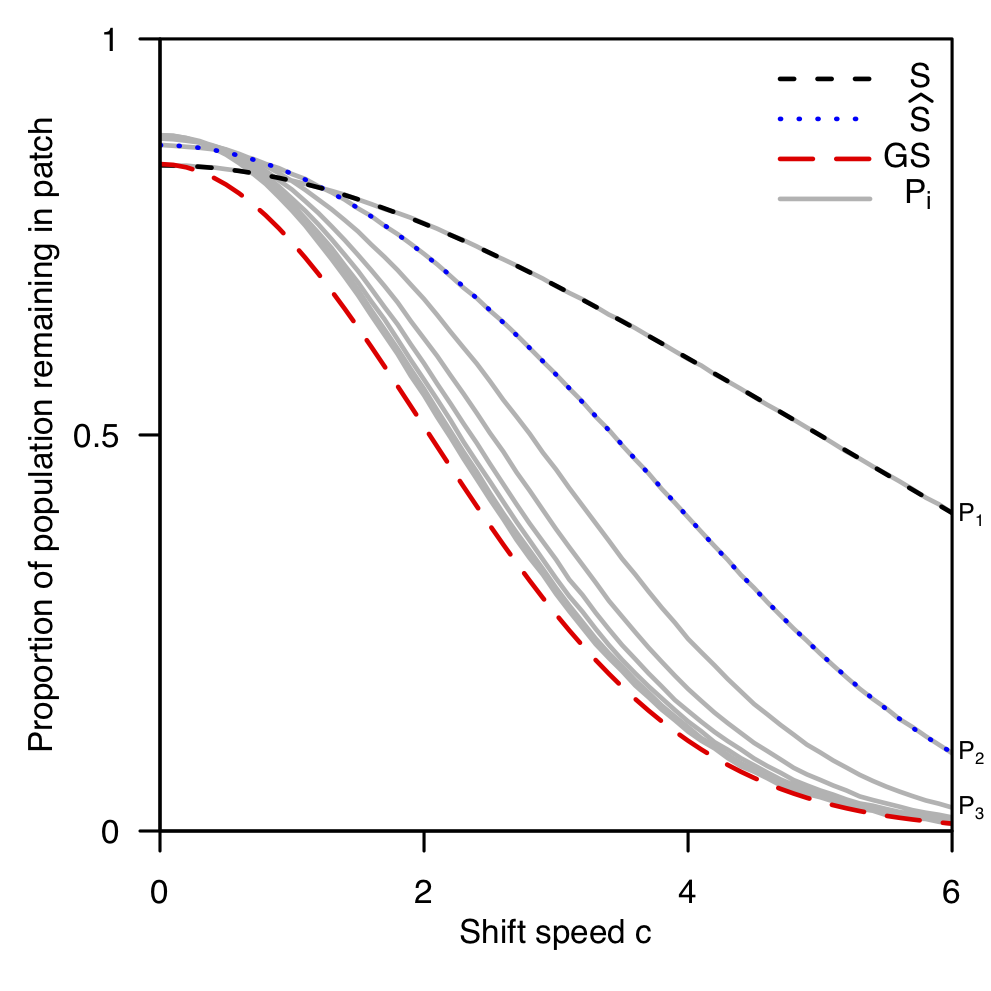
Asymmetric dispersal is a common trait among populations, often attributed to heterogeneity and stochasticity in both environment and demography. The cumulative effects of population dispersal in space and time have been described with some success by Van Kirk and Lewis’s average dispersal success approximation (Bull Math Biol 59(1): 107–137 1997), but this approximation has been demonstrated to perform poorly when applied to asymmetric dispersal. Here we provide a comparison of different characterizations of dispersal success and demonstrate how to capture the effects of asymmetric dispersal. We apply these different methods to a variety of integrodifference equation population models with asymmetric dispersal, and examine the methods’ effectiveness in approximating key ecological traits of the models, such as the critical patch size and the critical speed of climate change for population persistence.

A comparison of dispersal success metrics.
Figure 2: The proportions of eight generations of individuals remaining in a patch of length 10, assuming shifted Gaussian dispersal with $\sigma = 2$ and $c = 2$, averaged over 100 simulations. Each simulation began with initial population $N_0 = 1 000 000$ distributed randomly and uniformly across $\Omega$. After dispersal, each generation was bootstrapped back to the initial population size so that dispersal could be repeated indefinitely without running out of individuals. The proportion remaining after the first time step $P_1 = N_1/N_0$ is indistinguishable from the average dispersal success $S$. The ratio of populations between the first and second time step $P_2 = N_2/N_1$ is indistinguishable from the modified average dispersal success $\widehat{S}$. The sequence of population ratios between each successive time step $P_3, P_4, P_5, ...$ approaches the geometric symmetrization of average dispersal success $GS$.